“When it comes to writing code, the number one most important skill is how to keep a tangle of features from collapsing under the weight of its own complexity.”
~ James Hague

Day 25 of the May LeetCoding Challenge by Leetcode

Problem definition: Uncrossed Lines

We write the integers of A and B (in the order they are given) on two separate horizontal lines.

Now, we may draw connecting lines: a straight line connecting two numbers A[i] and B[j] such that:

• A[i] == B[j];
• The line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting lines cannot intersect even at the endpoints: each number can only belong to one connecting line.

Return the maximum number of connecting lines we can draw in this way.

Sample Testcase

Testcase 1

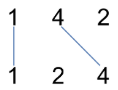
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.

Testcase 2

Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2]
Output: 3

Testcase 3

Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1]
Output: 2

Constraints:

• 1 <= preorder.length <= 100
• 1 <= preorder[i] <= 10^8
• The values of preorder are distinct.

I highly encourage you to attempt this problem on your own before looking at my solution.

Approach

Hint: Think dynamic programming. Given an oracle dp(i,j) that tells us how many lines A[i:], B[j:] [the sequence A[i], A[i+1], … and B[j], B[j+1], …] are uncrossed, can we write this as a recursion?

Solution

class Solution(object):
    def maxUncrossedLines(self, A, B):
        """
        :type A: List[int]
        :type B: List[int]
        :rtype: int
        """
        uncrossedLines = [[0] * (len(B) + 1) for i in range(len(A) + 1)]
        for i in range(1, len(A) + 1):
            for j in range(1, len(B) + 1):
                if(A[i - 1] == B[j - 1]):
                    uncrossedLines[i][j] = 1 + uncrossedLines[i - 1][j - 1]
                else:
                    uncrossedLines[i][j] = max(uncrossedLines[i - 1][j], uncrossedLines[i][j - 1])
        return uncrossedLines[len(A)][len(B)]

Submission Details

Total test cases passed: 74 / 74
Runtime: 168 ms
Memory Usage: 12.9 MB

Note: This submission was better than 73.18% of Python3 solutions in terms of runtime! Try to come up with a better approach! 🌚

I would really recommend you to explore this side of the Computer Science and tune in to the journey of competitive programming to write better, cleaner, efficient and optimal code! 😀

If you have a better approach to this problem, or for any other queries feel free to reach out to me! 😇